
0. 개요
이번에 통계학 배운게 심화 프로젝트에 쓰일 수가 있어서 통계학에 대해서 좀 정리를 해보려고 한다. 그에 앞서 머신 러닝의 과정과 함께해서 공부해야겠지만.... 일단은 차근차근 내용정리를 해야겠다.
1. 데이터의 종류
| 데이터 종류 | 개념 | 예시 |
| 수치형 | 숫자를 이용해 표현할 수 있는 데이터 이산형, 연속형을 모두 포함하는 개념 |
체중, 신장, 사고건수, 일 방문자수 |
| 연속형 | 일정 범위 안에서 어떤 값이든 취할 수 있는 데이터 | 체중, 신장 |
| 이산형 | 횟수와 값은 정수형 값만 취할 수 있는 데이터 즉, 소수점의 의미가 없는 데이터를 의미 (이는 연속형 데이터와 차이를 가진다.) |
사고건수, 일 방문자수 |
| 범주형 | 가능한 범주 안의 값만 취하는 데이터 = 값이 달라짐에 따라 좋다, 나쁘다고 할 수 없는 데이터 = 명목형 데이터 이진형과 순서형을 모두 포함하는 개념 |
나라, 도시, 혈액형, 성공여부, 등수, MBTI |
| 이진형 | 두개의 값만을 가지는 범주형 데이터의 특수한 경우 EX) 0과 1, 예/아니오, 참/거짓 |
성별, 성공여부 |
| 순서형 | 값들 사이에 분명한 순위가 있는 데이터 | 등 |

2 편차, 분산, 표준편차 정의
| 편차 (deviation) | 하나의 값에서 평균을 뺀 값 ➡️ 평균으로부터 얼마나 떨어져 있는지를 의미 |
| 분산(variation) | 편차의 합이 0으로 나오는 것을 방지하기 위해 생성된 개념 = 편차 제곱합의 평균 |
| 표준편차 (standard deviation) |
분산에 제곱근을 씌워준 값 ➡️ 원래 단위로 되돌리기 |
이러한 3개지의 개념을 쓰는 이유는 다음과 같다.
어떠한 두 분포가 있을 때, 아래의 그래프처럼 평균 혹은 중앙값 혹은 대표값은 달라도 데이터의 분포도가 다를 수 있다.

파란 그래프는 특정한 값이 많이 머물러 있는 것이며, 붉은 색 그래프는 여러 값들이 넓게 고루 분산된 형태이다.
해당 표는 어떠한 값들의 평균을 을 그린 그래프로서 이러한 방법으로는 데이터가 어떤지 완벽하게 말하기에는 어려움이 있기 때문이다.
다만, 평균/중앙값/최빈값은 데이터가 대략 어느정도 있는가를 표현해주는 거라면, 분산과 편차는 어떻게 존재하는 지에 대한 개념이라고 할 수 있다.
3. 모집단, 표본, 표본분포, 표준오차
| 모집단 | 어떤 데이터 집합을 구성하는 전체 대상 |
| 표본 | 모집단 중 일부, 모집단의 부분집합 |
| 표본분포 | 표본의 분포, 표본 통계량으로부터 얻은 도수 분포 |
| 표준오차 | 표본의 표준편차 = 표본평균의 평균과 모평균의 차이 EX) 모평균 70 , 표본평균 67 --> 표준 오차 3 |
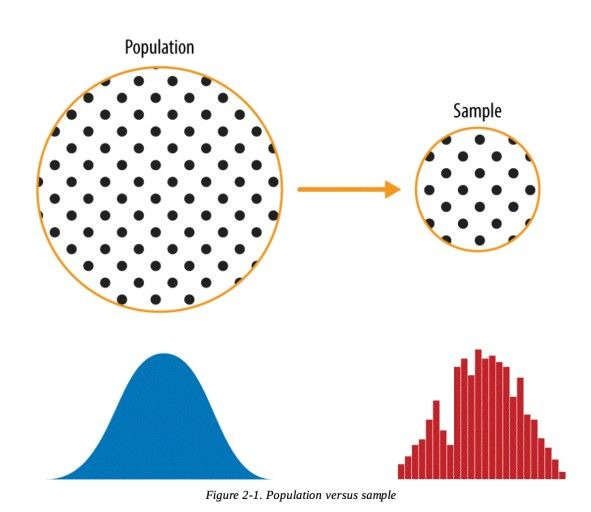
조사를 할 때, 모든 모집단을 뽑아낼 수 있다면 좋지만 모집단을 조사하는 것은 어려울 수 있다. 그 수가 많을 수가 있고, 계속해서 그 현상이 발생되기 때문이다. 다만, 모집단과 아주 유사한 것들만 모아볼 수 는 있는데 이를 표본 집단이다.
표본이 많아질 수록 모집단과 흡사해지는 경향이 있지만, 잘못된 표본은 모집단을 대표하지 못할 수 있으므로 이를 유의해야 한다.
표본 분포는 표본 통계량에서부터 얻은 도수분포로...
- 표본평균의 분포 : 모집단에서 표본집단을 추출하고 각 평균을 계산할 수록 중심극한정리에 의해서 정규 분포에 가까워 진다.
- 표본분산의 분포 : 모집단에서 표본집단을 추출하고 분산을 계산한다면 표본분산들의 분포는 카이제곱 분포를 따른다. 단, 모집단이 정규분포를 따를때 높게 성립된다.
4. 도수, 상대도수, 도수분포표
| 도수 | 특정 구간에 발생한 값의 수 |
| 상대도수 | 특정 도수를 전체 도수로 나눈 비율 |
| 도수분포표 | 각 값에 대한 도수와 상대도수를 나타내는 |
| 히스토그램 | 도수분포표를 활용해 만든 막대그래프 |
| 임의표본추출 | 무작위로 표본을 추출하는 것 |
| 편향 | 한쪽으로 치우쳐져 있음 |


5. 정규분포, 신뢰구간
중심 극한 정리 ➡️ 시간이 지나고, 모집단에 가까워 질수록 모든 값은 평균에 모여서 종모양을 이룬다. 평균에서 가장 그 확률이 높고, 평균에서 그 중심이 멀어지면서 나오는 모양을 정규 분포라고 한다.
‼️정규분포의 특징
- 분포는 평균을 중심으로 좌우 대칭의 형태다.
- 곡선은 각 확률값으로 나타나며, 더하면 +1이 된다.
- 정규분포는 평균과 분산(퍼진 정도)에 따라 다른 형태를 가진다.
- 평균 0, 분산 1을 가지는 경우 표준 정규 분포라고 한다.
✨정규분포에 대해서 학습해야하는 이유 ✨
각각의 그래프는 평균과 분산값에 따라서 다르게 그려진다. 이러한 경우에는 확률을 계산할 때 어려움을 겪게 된다. 따라서 이를 통일하기 위해 분포의 평균과 분산 값을 통일하는 작업을 하게 되는데 이를 표준화라고 한다.
| 표준화 공식 (Standard scaler) |
확률변수 X(값)에서 평균 m 을 빼고 표준편차로 나눈 값 |


6. 신뢰구간, 신뢰수준
모든 데이터는 표본을 추출하는 순간 불확실성을 가지게 되는데, 이는 표본이 무조건적으로 모집단 전체를 반영하지 못하기 때문이다. 따라서 우리는 이러한 데이터의 불확실성에 대해서 '신뢰도'가 높다/낮다로 이야기한다.
| 신뢰구간 | 특정 범위 내에 값이 존재할 것으로 예측되는 영역 |
| 신뢰수준 | 신제 모수를 추정하는 데 몇 퍼센트 확률로 신뢰구간이 실제 모수를 포함하게 되는 확률. 주로 95~99% 사이를 이용함 |
import scipy.stats as st
import numpy as np
#샘플 데이터 선언
sample1 = [5,10,17,29,14,25,16,13,9,17]
smaple2 = [21,22,27,19,23,24,20,26,25,23]
[신뢰구간 구하는 방법]
1. 신뢰구간을 구할때는 일반적으로 표준 오차를 사용한다.
➡️ 표준 편차 : 각 값이 평균으로부터 떨어진 정도
➡️ 표준 오차 : 표본 평균의 분포 표준편차
2. 표준편차를 통해 각 값이 평균으로부터 얼마나 떨어져 있는지 파악 후,
표준 오차를 통해 표본의 평균 값이 어느정도 정확하게 모집단의 평균을 추정하는 지
나타내주게 된다.
3. 이는 신뢰구간을 구하는 것이다.
df = len(sample1) -1 #자유도 : 샘플 개수 - 1
mu = np.mean(sample1) #표본 평균
se = st.sem(sample1) #표준 오차
#95% 신뢰구간
st.t.interval(0.95, df,mu,se)
#99% 신뢰구간
st.t.interval(0.99, df,mu,se)일단은 이론들 정리한 다음에 실습 정리를 차근차근 해야겠다. 오늘 늦게라도 발표 피드백한게 돌아와서, 발표대본이랑 함께 오늘 마저 올려두려고 한다.
아 피드백 보고 좀 무서웠다. 부족한거 아닐까? 랜덤 포레스트 모델을 내가 잘못안건? 회귀예측은 거의 맞았는데 이를 어떻게 설명했는지... 그게 부족했나 걱정된다. 앞으로의 팀에서도 잘 할수있을까? 미안해진다....
나도 불안이 많아서....ㅜ
'𝐓𝐈𝐋 (𝐅𝐨𝐫 𝐂𝐚𝐦𝐩) > 𝐂𝐎𝐃𝐈𝐍𝐆 (𝐒𝐐𝐋, 𝐏𝐘𝐓𝐇𝐎𝐍)' 카테고리의 다른 글
| [𝟐𝟓.𝟎𝟒.𝟏𝟔] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟖 (1) | 2025.04.16 |
|---|---|
| [𝟐𝟒.𝟎𝟒.𝟏𝟒] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟕 (0) | 2025.04.14 |
| [𝟐𝟓.𝟎𝟒.𝟎𝟐] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟓 (0) | 2025.04.02 |
| [𝟐𝟓.𝟎𝟒.𝟎𝟏] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟒 (0) | 2025.04.01 |
| [𝟐𝟓.𝟎𝟑.𝟑𝟏] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟑 (1) | 2025.03.31 |