
0. 개요
오늘 파이썬(통계랑 오늘 라이브 세션으로 들은 것)과 관련해서 좀 정리해보려고 한다.
1. 모집단과 관련된 파이썬 실습 정리
[모집단과 표본 집단]
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000) --> 모집단 인구 생성(전체 인구)
# 표본 추출
sample = np.random.choice(population, 100) --> 랜덤값에서 population 에서 추출
plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')
plt.show()## numpy.random 함수란?
numpy.random 모듈 ➡️ Numpy 라이브러리의 일부, 다양한 확률 분포에 따라 난수를 생성하는 기능
[데이터 분석, 시뮬레이션 방법 등 다양한 분야에서 사용]
np.random.normal ➡️ 함수는 정규분포(가우시안 분포)를 따르는 난수를 생성 **가우시안 분포 = 정규 분포
numpy.random.normal(loc=0.0, scale=1.0, size=None)
##loc(float) ➡️ 정규분포의 평균(기본값 0.0)
##scale(float) ➡️ 정규분포의 표준편차(기본값 1.0)
##size(int 또는 tuple of int) ➡️ 출력 배열의 크기(기본값: None, 즉 스칼라값의 변환)np.random.choice ➡️ 주어진 배열에서 임의로 샘플랑하여 요소를 선택 (지정된 배열에서 무작위로 선택된 요소를 반환)
numpy.random.choice(a, size=None, replace=True, p=None)
##a(1-D array-like or ints) ➡️ 출력 배열의 크기(기본값: None, 즉 단일값 반환)
##size(int 또는 tuple of ints) ➡️ 출력 배열의 크기(기본값: None, 즉 단일값 반환)
##replace(boolean)➡️ 복원 추출여부를 나타냄 (True = 동일한 요소가 여러번 선택될 수 있음)
➡️ 기본값은 True
##p(1-D array-like,optional) ➡️ 각 요소가 선택될 확률. 배열의 합은 1.plt.hist ➡️ 라이브러리 에서 히스토그램을 그리는 함수 (히스토그램, 데이터의 분포를 시각화 하는데 유용하다.)
1) bins ➡️ 히스토그램의 (bins)의 갯수 또는 경계 | 데이터 몇개의 구간을 나눌 것인지에 대한 것 | 정수나 리스트로 입력함
2) alpha ➡️ 히스토그램 막대의 투명도를 지정 (0(투명)~1(불투명) 사이의 값)
3) label ➡️ 히스토그램의 레이블 지정 | 여러 히스토그램을 그릴때 범례를 추가하는데 사용
4) color ➡️ 히스토그램의 색상을 지정

2. 표본오차와 신뢰구간
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")scipy.stats ➡️ SciPy 라이브러리의 일부, 통계분석을 위한 다양한 함수와 클래스를 제공하는 모듈
spicy.stats.t.interval ➡️ 주어진 수준에서 t-분포를 사용해 신뢰구간을 계산하는 데 사용
scipy.stats.t.interval(alpha, df, loc=0, scale=1)
##alpha ➡️ 신뢰수준을 의미합니다. 95% 신뢰수준을 원하면 0.95를 입력
##df ➡️ 자유도(degrees of freedom), 일반적으로 표본 크기에서 1을 뺀 값으로 설정
(df = n-1)
##loc ➡️ 위치(parameter of location), 일반적으로 표본 평균을 설정
##scale ➡️ 스케일(parameter of scale)로, 일반적으로 표본 표준 오차를 설정
➡️ 표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값
(scale = sample_std / sqrt(n))
3. 정규분포 파이썬 실습
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim() --> 수평선추가히는 과정[x축이 표시되는 범위를 지정]
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10) --> 정규분포의 함수
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()
4. 긴 꼬리 분포
# 긴 꼬리 분포 생성 (예: 소득 데이터)
long_tail = np.random.exponential(1, 1000)
# 히스토그램으로 시각화
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='b')
plt.title('long tail distribution histogram')
plt.show()
5. 스튜던트 t 분포
# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)
# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')
# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
➡️ [구간 시작점, 구간 끝점, 구간 내 숫자 갯수]|끝점 미포함(endpoint = False)|숫자 사이의 간격(retstep = True)
p = stats.t.pdf(x, df=10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
plt.show()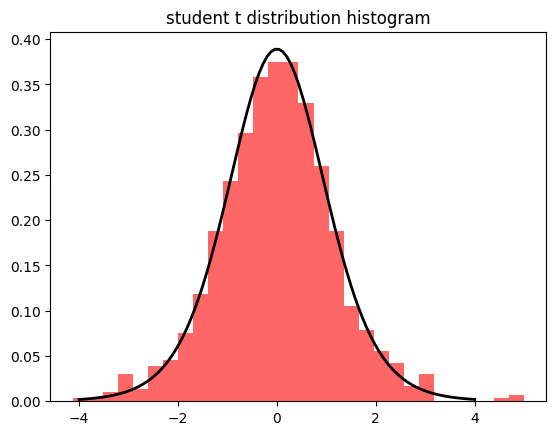
6. 카이제곱분포
# 카이제곱분포 생성
chi2_dist = np.random.chisquare(df=2, size=1000)
# 히스토그램으로 시각화
plt.hist(chi2_dist, bins=30, density=True, alpha=0.6, color='m')
# 카이제곱분포 곡선 추가
x = np.linspace(0, 10, 100)
p = stats.chi2.pdf(x, df=2)
plt.plot(x, p, 'k', linewidth=2)
plt.title('chi2 distribution histogram')
plt.show()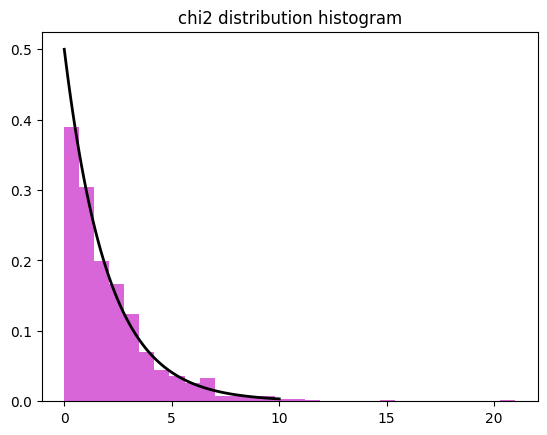
7. 이항 분포
# 이항분포 생성 (예: 동전 던지기 10번 중 앞면이 나오는 횟수)
binom_dist = np.random.binomial(n=10, p=0.5, size=1000) --> 이항분포에만 사용하는 함수
# 히스토그램으로 시각화
plt.hist(binom_dist, bins=10, density=True, alpha=0.6, color='y')
plt.title('binomial distribution histogram')
plt.show()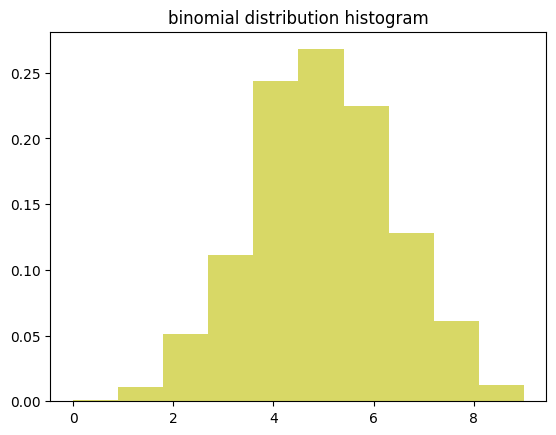
8. 푸아송 분포
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson --> 푸아송 분포를 만들 수 있는 기능
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
##이외에도 np.random.poisson(lam,size)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='b', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()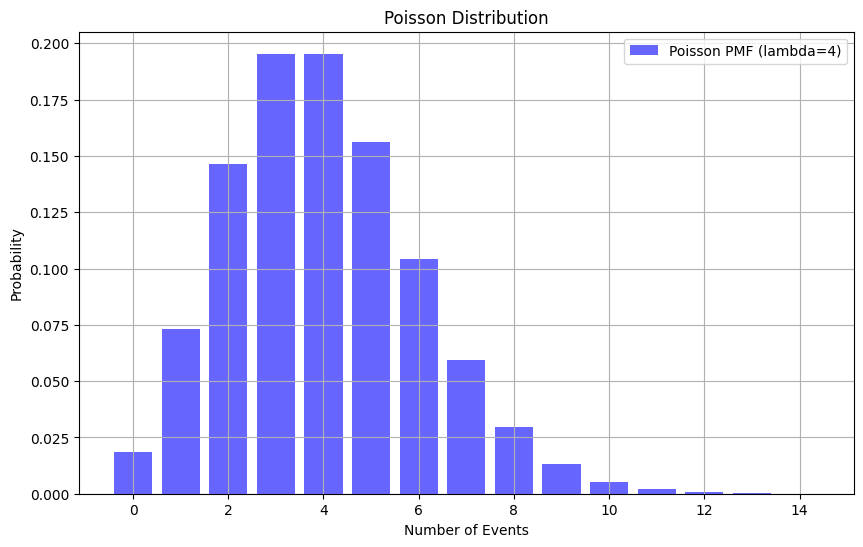
일단 무작위 추출해서 좀 정리해보자면 이렇게 가져올 수 있을 거 같다.
| 이산적인 가능성이 있는 분포 (어떠한 연속성을 가지기보다는 불연속적인 데이터를 가지고 있는 데이터들) |
연속적인 가능성이 있는 분포 (데이터 자체에 어떠한 연속성이 부여되어 있는 경우를 말함) |
| 이항분포(binomial distribution) ➡️ np.random.binomial(n,p,size) |
정규분포(normal distribution) ➡️ np.random.normal(loc,scale,size) |
| 초기하분포(Hypergeometric distribution) ➡️ np.random.hypergeometric(ngood, nbad, nsmaple, size) |
t-분포(t-distribution) ➡️ np.random.standard_t(df,size) |
| 푸아송분포(Poisson distribution) ➡️ np.random.poisson(lam,size) |
균등분포(uniform distribution) ➡️ np.random.uniform(low,high,size) |
| F-분포(F-distribution) ➡️ np.random.f(dfnum,dfden, size) |
일단은 파이썬 실습한 것도 혹시 몰라서 기록을 남겨두는데...
아, 통계 라이브 세션을 오늘 배가 아파서 계속 못들었다. 너무 속상해서 내일 이어서 들으려고 한다.
이번에 모집단과 표준 편차에 대해서 들었기도 하니까, 그건 통계학에서 가장 중요한 개념이기도 하니까. 그래서 다음 TIL 이랑 함께 파이썬 에서 배운거 복습도 해보려고 한다.
'𝐓𝐈𝐋 (𝐅𝐨𝐫 𝐂𝐚𝐦𝐩) > 𝐂𝐎𝐃𝐈𝐍𝐆 (𝐒𝐐𝐋, 𝐏𝐘𝐓𝐇𝐎𝐍)' 카테고리의 다른 글
| [𝟐𝟓.𝟎𝟒.𝟎𝟏] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟒 (0) | 2025.04.01 |
|---|---|
| [𝟐𝟓.𝟎𝟑.𝟑𝟏] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟑 (1) | 2025.03.31 |
| [𝟐𝟓.𝟎𝟑.𝟑𝟎] 𝐖𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟐 (0) | 2025.03.31 |
| [𝟐𝟓.𝟎𝟑.𝟏𝟗] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟏 (0) | 2025.03.19 |
| [𝟐𝟓.𝟎𝟑.𝟏𝟖] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟎 (0) | 2025.03.18 |
