
0. 개요
오늘 읽어던 아티클 스터디랑 통계학 표준 분포에 대해서 정리해보려고 한다. 오늘은 분포와 관련해서 이것저것 들었다.
1. 아티클 스터디
파이썬 초보자가 저지르는 10가지 실수 | 요즘IT
파이썬을 처음 배울 때, 우리는 자신도 모르게 몇 개의 나쁜 코딩 습관들을 갖게 됩니다. 처음에는 문제없이 작동했지만, 나중에 정상적으로 작동하지 않거나 뒤늦게 문제를 더 쉽게 해결할 수
yozm.wishket.com
☑️ 요약 : 파이썬을 효과적으로 다루는 방법
1. import * 사용 → import 하는 객체가 어떤 것인지 정확하기 명시합니다.
2. except 절 사용 → 어떠한 절을 예외시킬지 확실하게 합니다.
3. numpy 함수 사용 → numpy 는 수학계산에 사용. for 보다 더욱 효율적이다. (함수 코드의 길이가 줄어들음)
4. 이전에 연 파일들을 닫을 것 → 열린 데이터가 닫히지 않으므로 with 를 사용하여 파일을 정상적으로 닫을 것
5. pep8의 가이드를 벗어나지 말것 → 이해하기 쉽게 간결하게 작성하세요.
6. 딕셔너리의 keys, values 를 알맞게 사용할 것 → 하나씩 지정할 필요 없이 key 와 value 만으로 검색이 가능함.
7. comprehension 의 사용은 적절히 →
comprehesion = 정의된 시퀀스를 기반으로 새 시컨스를 생성할 때 도움이 된다. for 보다 더 간결히 쓸 수 있다.
8. range(len()) 보다는 enmerate 를 상요해 단순화 할 것 (두개의 리스트는 zip 을 사용)
9. + 연산자 보디는 f 스트링의 사용으로 코드를 간결히 하는 것이 좋다.
10. mutable value(가변성 value ⇒ 바꿀 수 있는 value 값)를 디폴트 매개로 사용하지 말 것 → none 으로 설정해 필요한 코드만을 빼옵니다.
☑️ 결론적으로 복잡하고 다양한 함수식을 사용하는 것보다는 간결하고, 이해가 쉬운 코드로 프로그램 연산자를 사용하는 것이 도움이 된다.
- 주요 포인트 :
파이썬 코드를 효율적으로 쓰는 방법에 대해서 알아봅니다.
- 인사이트 :
결론적으로 파이썬 문구를 작성하는 데에 있어서 간결하고 가독성 있는 깔끔한 문장구조를 쓸 필요가 있음
→ **기획자도 파이썬을 배워야하나요?** 라는 칼럼에서도 파이썬 사용의 이유는 정확하고 빠른 데이터 분석을 위한 것이였음
→ 다만, 자신이 알아볼 수있는 개별의 코드 작성도 필요하나, 그것이 불가능하다면 **소통비용을 줄이기 위해** 보다 간결하고 깔끔하게 이를 작성할 수 있어야함
→ 비효율적인 이유 : 1개로 정의할 수 있는 코드를 여러개의 코드로 연산하게 해서 계산 시간을 복잡하게 한다.
2. 모집단과 표본 집단
➡️ 정의
모집단 - 관심이 대상이 되는 전체 집단
표본 집단 - 모집단에서 추출한 집단의 일부
➡️ 사용하는 이유
1. 현실적인 제약
➡️ 비용과 시간 - 전체 모집단을 모으는 것은 시간과 비용이 들며, 불가능하다. (표본집단이 그래도 자원을 절약)
➡️ 접근성 - 모든 데이터를 수집하는 것은 불가능하다.
2. 표본의 대표성
➡️ 잘 설계된 표본은 모집단의 특성을 반영 가능
➡️무작위로 표본을 추출하면 편향을 최소화하고 모집단의 다양한 특성을 포함할 수 있음
3. 데이터 관리
➡️ 데이터 처리의 용이성 : 표본 데이터를 사용하는 것이 전체 데이터를 다루는 것보다 데이터의 처리, 분석 용이
➡️ 데이터 품질 관리 : 작은 표본에서 데이터 품질을 더 쉽게 관리하고, 오류나 이상값을 식별해 수정 가능
4. 모델 검증 용이
➡️ 모델 적합도 테스트 : 표본 데이터를 사용해 통계적 모델을 검증할 수 있음
➡️ 모델이 표본 데이터에 잘 맞는다면, 모집단에도 잘 맞을 가능성 있음
3. 표본 오차와 신뢰 구간
| 표본 오차 | 신뢰 구간 | |
| 정의 | 표본에서 계산된 통계량과 모집단의 진짜 값 간의 차이 | 모집단의 특정 파라미터(예: 비율,평균)에 대해서 추정된 값이 포함될 것으로 기대되는 범위 |
| 특징 | ➡️ 표본 크기가 클수록 표본오차는 작아짐 ➡️ 표본이 모집단을 완벽하게 대표하지 못하기 땜누에 발생 ➡️ 표본 크기와 추출 방법에 따라서 달라짐 - 표본 크기 : 크기가 클수록 오차가 줄어듬 (더 많은 데이터일수록 모집단을 대표함) - 표본 추출 방법 : 무작위 추출방법 사용시 표본 오차를 줄일 수 있음 (모든 모집단 요소를 선택할 동등한 기회 제공) |
➡️신뢰구간 계산 방법 ➡️신뢰구간 = 표본평균±z×표준오차 ➡️z = 선택된 신뢰수준에 해당되는 z-값 일반적으로 95%의 신뢰수준을 많이 사용한다. |

| 표본 분포 | 신뢰구간 시각화 | |
| 붉은 색 점선 : 모집단의 평균 파란색 점선 : 표본의 평균 |
파란색 점선 : 표본의 평균 녹색 점선 : 95% 신로구간의 상한과 하한 |
|
| ➡️ 모집단의 분포는 넓고, 표본 평균들의 분포는 좁아진다. ➡️ 표본 크기가 커질수록 표본 평균이 모집단 평균에 더 가까워지는 경향을 보여줌 |
➡️ 오른쪽 그림 - 표본의 분포와 신뢰구간 95%를 보여줌 ➡️ 모집단의 평균을 포함할 것으로 예상되는 범위(신뢰구간) |
4. 정규 분포

| 정규분포 | |
| 정의 | ➡️ 종 모양의 대칭 분포, 데이터가 평균 주의에 머무름 ➡️ 평균을 중심으로 좌우 대칭, 평균에서 멀어질 수록 데이터 빈도 줄어듬 ➡️ 분포의 퍼짐 정도를 나타냄 |
| 특징 | 대부분 데이터가 평균 주변에 몰려 있으며 평균에서 멀어질 수록 빈도가 준다 |
5,. 긴 꼬리 분포

| 긴 꼬리 분포 | |
| 정의 | ➡️ 대부분의 데이터가 분포의 한쪽 끝에 몰려있고, 반대쪽으로 긴 꼬리가 이어지는 형태의 분포 ➡️ 대칭적이지 않고 비대칭적 ➡️ 특정한 하나의 분포를 의미하지 않으며, 여러 종류의 분포(ex. 파레토 분포, 지프의 법칙, 멱함수)를 포함할 수 있음 |
| 특징 | 소득 분포, 웹사이트 방문자 수 등에서 관찰되며, 부동산 실거래가도 여기에 해당됨 |
6. 스튜던트 t 분포

| 스튜던트 t 분포 | |
| 정의 | 모집단의 표준편차를 알 수 없고, 표본의 크기가 작은 경우(일반적으로 30미만)에 사용되는 분포를 이르는 말 |
| 특징 | ➡️ 정규분포와 유사하지만 표본의 크기가 작을 수록 두꺼워지는 특징 ➡️ 표본의 크기가 커지면 정규분포에 가까워짐 |
7. 카이제곱분포

| 카이제곱분포 | |
| 정의 | 범주형 데이터의 독립성 검정이나 적합도 검정에 사용되는 분포 |
| 특징 | ➡️ 자유도 모양에 따라 모양이 달라짐 ➡️ 상관관계, 인과관계를 판별하고자 하는 원인의 독립변수가 완벽하게 서로 다른 질적 자료 일때 활용한다 ➡️ 범주형 데이터 분석에 사 |
| 독립성 검정 | 두 범주형 변수 간의 관계가 있는지 확인할 때 사용 |
| 적합도 검정 | 관측한 값들이 특정 분포에 해당하는지 검정할 때 사용 |
8. 이항분포
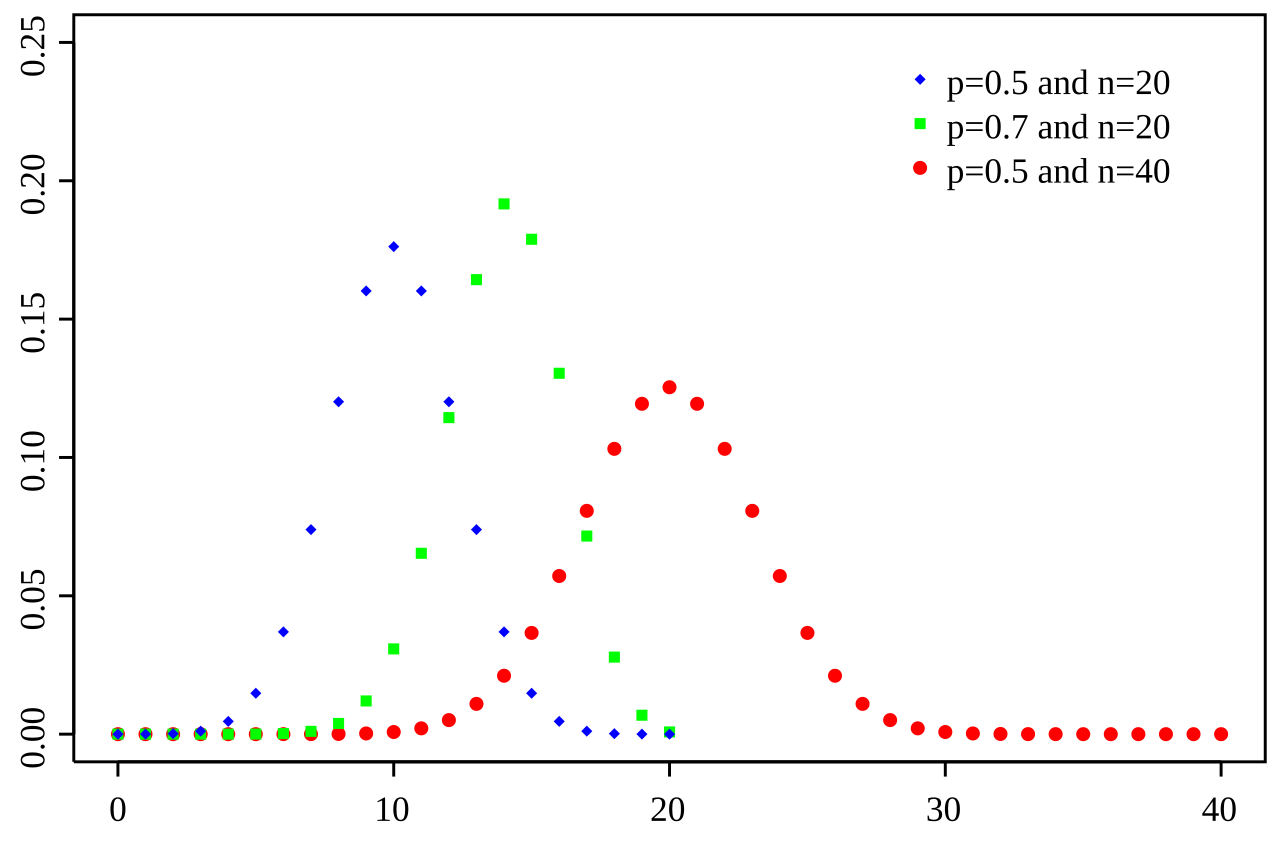
| 이항분포 | |
| 정의 | 연속된 값을 가지지 않고 특정한 정수값만을 가지는 분포 성공/실패와 같은 두가지 결과를 가지는 실험을 여러번 반복했을 떄 성공횟수의 분포 |
| 특징 | ➡️ 독립적인 시행이 N번 반복되고, 각 시행에서 성공과 실패 중 하나의 결과만 가능한 경우만 모델링 하는 경우를 말함 ➡️ 성공 확률이 p 라 할때, 성공 횟수를 확률적으로 나타냄 ➡️ 실험횟수(n)와 성공확률(p)로 정의 |
9. 푸아송 분포

| 푸아송 분포 | |
| 정의 | 단위 시간 또는 단위 면적 당 발생하는 사건의 수를 모델링 할 때 사용하는 분포 |
| 특징 | ➡️ 이산형 분포에 해당(연속된 값을 가지지 않음) ➡️ 평균 발생률 λ(람다)가 충분히 크면 정규 분포에 가까워짐 ➡️ 평균 발생률 λ를 가진 사건이 주어진 시간 또는 공간 내에서 몇번 발생하는 지 나타냄 ➡️ 단위 시간 또는 단위 면적당 희귀하게 발생하는 사건의 수를 모델링하는데 적합 |
10. 정리
데이터 수가 많아지면 정규분포에 가까워진다 (중심 극한 정리)
➡️ 데이터 수가 많으면 정규분포에 가까워진다
➡️ 데이터가 적다면 각 상황에 맞는 분포를 선택한다
➡️ 데이터가 적을 수록 각 상황에 맞는 분포를 선택
| 분포를 고르는 기준 | |
| 종류 | 정규 분포 ➡️ 데이터 수가 충분하다 스튜던트 t 분포 ➡️ 데이터 수가 적다 롱 테일 분포(파레토 분포) ➡️ 일부 데이터가 전체적으로 영향을 미친다 카이 제곱 분포 ➡️ 범주형 데이터의 독립성 검정이나 적합도 검정 이항 분포 ➡️ 결과가 두개만 나오는 상황 푸아송 분포 ➡️ 특정 시간, 공간에서 발생하는 사건 |
내일은 이 내용들과 관련된 시각화 파이썬 실습을 정리해보려고 한다. 이번에 베이직 반으로 들었는데, 이것도 따라가기 어렵다는 생각이 들더라. 조금 메모를 열심히 해서 아자아자 힘을 내야겠다!
'𝐓𝐈𝐋 (𝐅𝐨𝐫 𝐂𝐚𝐦𝐩) > 𝐂𝐎𝐃𝐈𝐍𝐆 (𝐒𝐐𝐋, 𝐏𝐘𝐓𝐇𝐎𝐍)' 카테고리의 다른 글
| [𝟐𝟓.𝟎𝟒.𝟎𝟐] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟓 (0) | 2025.04.02 |
|---|---|
| [𝟐𝟓.𝟎𝟑.𝟑𝟏] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟑 (1) | 2025.03.31 |
| [𝟐𝟓.𝟎𝟑.𝟑𝟎] 𝐖𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟐 (0) | 2025.03.31 |
| [𝟐𝟓.𝟎𝟑.𝟏𝟗] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟏 (0) | 2025.03.19 |
| [𝟐𝟓.𝟎𝟑.𝟏𝟖] 𝐓𝐈𝐋 𝐍𝐎𝐓𝐄 𝟐𝟎 (0) | 2025.03.18 |
